HTML5 미니게임 개발 튜토리얼
이전 글 : Swing my baby 를 통해 보는 HTML5 게임 개발(1)
Swing my baby 를 통해 보는 HTML5 게임 개발(2)
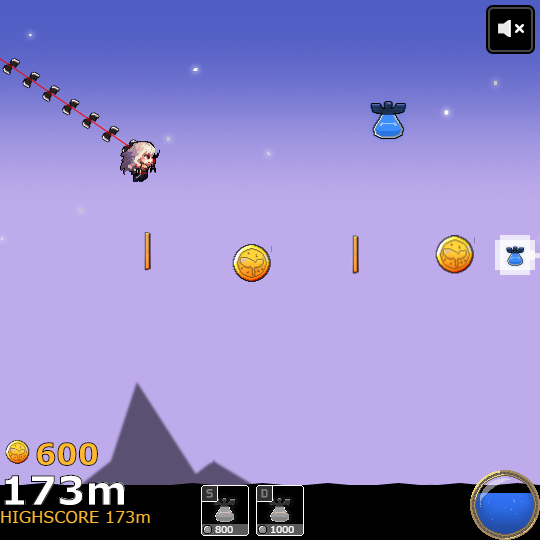
개발 과정
캐릭터 만들기
진자의 움직임 적용
이제 이 게임의 핵심인 줄타기를 만들어보자. 이것만 되면 게임 자체의 메커니즘은 거의 완성이다. 나머지는 부차적인 부분일 뿐... 우리의 이 게임에서는 유저가 스페이스바를 누를 때마다 캐릭터가 줄을 걸고 줄에서 점프하기를 반복해야 한다. 입력 처리는 이후에 다시 나올테니까 우선 줄을 걸어서 캐릭터가 움직이도록 해보자.
일단 줄을 걸어보자
현재 캐릭터는 x 와 y 좌표만을 가지고 있는데, 줄을 걸게 되면 "줄이 걸린 위치"를 나타낼 변수가 필요하다.
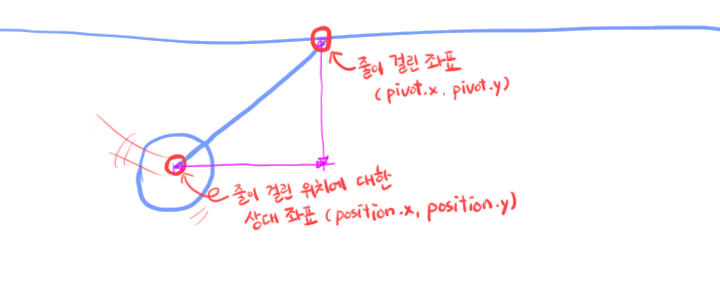
그럼 이 좌표들을 나타낼 변수를 추가해보자.
Character.init 메소드를 아래처럼 변경한다.
init(){
// 여기서는 각종 변수를 초기화해야 한다.
// 일단 현재 위치를 나타내는 변수를 만들어봤다.
this.x = 0;
this.y = 0;
this.gravity = 10; //일단 대충 10으로 해보자.
this.pivot = null; //이건 줄이 걸린 좌표를 나타내는 변수다. null 이면 안 걸린거
this.position = null; //이건 줄에 대한 캐릭터의 상대 좌표
this.pLen = 0; //이건 줄의 길이
this.angle = 0; //현재 진자운동의 각도
this.accel = 0; //현재의 각가속도
}
줄의 길이가 왜 필요한가? 이건 잠시후에 진자의 물리학에서 살펴보자.
줄 걸기
줄을 걸 수 있는 변수가 생겼으니 줄을 거는 메소드를 만들어보도록 하자.
setPivot(point){
//point 로 지정된 곳에 줄을 건다
if( this.pivot === null ){
// 현재 줄이 걸리지 않은 상태일때만 줄을 건다
this.pivot = point; // 지지점을 할당하고
this.pLen = Math.distance(this, this.pivot); // 줄 길이
this.position = {x:this.x - this.pivot.x, y:this.y - this.pivot.y}; // 상대위치
this.angle = Math.angle({x:this.x, y:this.y}, this.pivot); // 현재 각도
this.accel =
(-1.0 * (this.force.x+this.force.y)/this.pLen) * Math.sin(this.angle); // 각가속도
this.update(0); // 줄이 걸린 것을 바로 반영하기 위해 업데이트 한 번 호출해준다.
}
}
Math.distance나
Math.angle은 바로 밑에서 추가할테니 넘나 새롭다고 놀라지 말고 침착하게 읽어 보자.
수학 계산 유틸리티
그럼 이제부터 진자운동을 계산해보도록 하자. 그 전에 계산하기 쉽도록 몇가지 유틸리티 함수를 만들면 편하다. 아래 내용을 array.prototype.last 만든 곳 밑에다가 넣자. 하기 전에 일단 피타고라스 아저씨한테 잠시 감사를..
Math.distance = function(p1, p2){
// 두 점 간의 거리를 구하는 함수
// 왜 아래처럼 되는지 궁금하면 피타고라스의 정리를 보도록 하자!
return Math.abs(Math.sqrt(Math.pow(p2.x-p1.x,2) + Math.pow(p2.y-p1.y,2)));
}
Math.rad2deg = function(rad){
// 라디안 각도를 60분법 각도로 변환
return rad * 180 / Math.PI;
}
Math.deg2rad = function(deg){
// 60분법 각도를 라디안으로 변환
return deg / 180 * Math.PI;
}
Math.angle = function(p1,p2){
// 두 지점의 각도를 구하자
let w = p2.x - p1.x;
let h = p2.y - p1.y;
return Math.atan2(-h,w) - Math.PI/2;
}
Math.getPoint = function(pt, deg, len){
// 한 점에서 특정 각도로 특정 거리 떨어진 점의 좌표를 구한다
return {x:pt.x + (len*Math.cos(deg)), y:pt.y + (len*Math.sin(deg))};
}
Math.angle 에서 단순히 Math.atan2(h,2); 를 반환하지 않고 -h 와 (-Math.PI/2) 를 해주는 이유는...
이렇게 우리가 원하는대로 각도를 얻어오기 위해서 구해진 값을 조작해야 할 필요가 있기 때문이다.
진자의 물리학
일단 이 글을 쓰기에 앞서서 나는 가방끈도 짧고 수학도 젠젠 모른다는 점을 명시해두도록 하자. 아래 내용 중에 틀린게 있거나 비효율적인게 있을수도 있으니 대충 '아 얘는 이따위로 이걸 만들었구나..'라고 생각하도록 하자. 물론 더 좋은 공식이나 방법이 있다면 댓글로 알려주면 남들에게도 도움이 될 지도 모른다...(보는 사람이 있다면 말이지만)
우리의 캐릭터는 x 축에 대한 힘과 y 축에 대한 힘만을 가지고 이동한다. 따라서 진자 운동의 각속도를 x 축과 y축 선분으로 분해해서 캐릭터에 적용해주면 깔끔하게 캐릭터의 진자운동을 근사할 수 있게 된다.
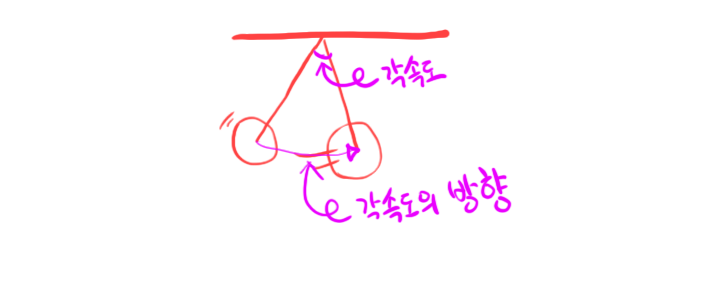
우리가 진자운동에서 신경써야 할 유일한 부분은 바로 이 각속도다. 프레임당 각속도만 계산할 수 있으면 나머지는 다 무시해도 된다. 그럼 이 각속도는 어떻게 구해질까?
현재 진자 추에 가해지는 각가속도 = (중력/진자 줄의 길이)*sin(현재 진자의 각도)
대충 이렇게 구하면 현재 위치에서의 각가속도가 나온다. 그럼 이걸 또 어떻게 적용할까?
Character.update 에서 진자의 현재 위치에서의 각가속도를 구해서 진자 각도에 더해주도록 하자. 그걸로 현재 캐릭터의 지지점에 대한 상대위치는 간단히 결정할 수 있다. 그리고 이렇게 구해진 가속도를 가지고 가로세로 힘으로 분해해서 force 를 계산하고, 해당 force를 캐릭터의 위치에 반영하면 된다.
update(timeDelta){
// 캐릭터의 각종 상태를 변경하는 부분.
if(this.pivot === null){
// 줄이 걸려있지 않을때
this.force.y += this.gravity * timeDelta;
this.x += this.force.x;
this.y += this.force.y;
}else{
// 줄이 걸려있을 때
// 중력은 작용하고 있지만 각가속도 계산에 들어가므로 force.y 에 별도로 더해줄 필요가 없다.
let ang = this.angle;
let ang_vel = (-1*this.gravity/this.pLen) * Math.sin(ang); //각가속도
// 현재 각가속도에 경과시간을 곱해서 전체 각가속도에 합산
this.accel += ang_vel * timeDelta;
// 계속 같은 높이로 흔들릴 수는 없으니 시간이 흐를수록 가속도를 줄여준다.
// 현실로 치자면 줄의 마찰력이나 공기저항에 대한 시뮬레이션이라고 볼 수 있겟지?
this.accel *= 0.999;
// 그럼 이제 다음번 각속도 계산을 위해 현재 각도를 바꿔주고
ang += this.accel;
this.angle = ang;
// 각 성분으로 분해해서 force에 할당하자
this.force.x = this.pLen * this.accel * Math.cos(ang);
this.force.y = this.pLen * this.accel * Math.sin(ang);
this.position.x += this.force.x;
this.position.y += this.force.y;
}
}
진자가 걸려있으면 줄이 표시되어야 한다. 줄 표시를 넣고, force가 제대로 들어가는지도 확인할 수 있도록 force를 눈으로 볼 수 있게
Character.render를 아래와 같이 고쳐보자.
render(ctx){
// 여기서 그려주면 된다.
ctx.save();
if( this.pivot !== null ){ // 줄이 걸려있으면 줄을 그려준다
ctx.strokeStyle = "blue";
ctx.beginPath();
ctx.moveTo(this.pivot.x, this.pivot.y);
ctx.lineTo(this.pivot.x+this.position.x, this.pivot.y+this.position.y);
ctx.stroke();
}
ctx.translate(this.x, this.y);
ctx.fillStyle = "red";
ctx.beginPath();
ctx.arc(0, 0, 20, 0, 2*Math.PI); // 각도는 늘 라디안이라는 점을 잊지 말자!
ctx.fill();
// force를 확인하기 쉽도록 20배로 증폭해서 화면에 그려준다
ctx.fillStyle = "black";
ctx.fillRect(0, 0, 2, this.force.y*20);
ctx.fillRect(0, 0, this.force.x*20, 2);
ctx.restore();
}
이렇게 하면 force 의 각 성분을 20배로 증폭해서 선 모양으로 볼 수 있게 된다.
이렇게 열심히 만들었으니까 정말 잘 동작하는지 테스트를 해봐야겠지?
GameScene.update에 아래와 같은 내용을 추가해보자
update(timeDelta){
super.update(timeDelta);
// 0.5초 이후에 줄을 걸어보자
if( this.elapsed > 0.5 && this.character.pivot === null){
this.character.setPivot({x:240, y:0}); //240,0 좌표로 줄 걸기!
}
}
여기까지 진행하면 아래와 같이 귀요미 진자가 동작하는 것을 볼 수 있다! 뿌듯행!
잠시 쉰다는 마음으로 여러가지 값들을 바꿔보면서 한껏 즐겨주자! 헤헿
진자에서 탈출하려면
자 이렇게 줄을 걸어서 매달리는건 구현이 되었는데... 이제 이 줄에서 탈출을 해야겠지? 사실 탈출하는건 어렵지 않다. 그냥 this.pivot = null; 만 넣어주면 바로 탈출이 된다.
setPivot을 고쳐보자.
setPivot(point){
//point 로 지정된 곳에 줄을 건다
if( this.pivot === null ){
// 현재 줄이 걸리지 않은 상태일때만 줄을 건다
this.pivot = point; // 지지점을 할당하고
this.pLen = Math.distance(this, this.pivot); // 줄 길이
this.position = {x:this.x - this.pivot.x, y:this.y - this.pivot.y}; // 상대위치
this.angle = Math.angle({x:this.x, y:this.y}, this.pivot); // 현재 각도
this.accel =
(-1.0 * (this.force.x+this.force.y)/this.pLen) * Math.sin(this.angle); // 각가속도
this.update(0); // 줄이 걸린 것을 바로 반영하기 위해 업데이트 한 번 호출해준다.
}else{
this.pivot = null;
this.pLen = 0;
this.position = null;
this.angle = 0;
this.accel = 0;
this.update(0);
}
}
다른 변수들도 그냥 마음이 상쾌하도록 같이 초기화를 시켜봤다. 실제로는 안 해줘도 된다.
예외처리
진자운동을 하다 보면 혹시 넘나 쎄게 매달려서 앞뒤로 90도 이상 흔들리는 경우도 있게 된다. 심하면 진자 운동이 아니라 한 방향으로 뱅글뱅글 돌게 될 수도 있다. 우리가 만든 공식으로 이런 부분도 제대로 표현되긴 하지만, 큰 문제가 있다. 현실에서 줄로 매달린 경우에, 진폭이 180도를 넘어가게 되면 줄이 강체가 아닌 이상 약간씩 궤도가 흐트러지게 마련이다. 하지만 우리가 만든 공식은 줄을 완벽한 강체로 가정하고 동작한다. 말하자면 우리의 코드상에서 줄은 사실 줄이 아니라 막대기와 비슷한 물체다.
그러면 어떻게하면 사실적으로 줄을 시뮬레이션할 수 있을까? 정답은 간단하다. 안 하면 된다.
앞이건 뒤건 진자의 각도가 90도를 넘으면 천장에 머리를 박고 떨어지게 만들자ㅋㅋㅋ
업데이트에서 ang += this.accel; 줄 바로 밑에 아래와 같이 추가하자.
if( Math.abs(Math.rad2deg(ang)) >= 90 ){
this.setPivot(null);
return;
}
그러면 이제 각도가 -90 이상이거나 90 이상이면 줄에서 자동으로 떨어지게 된다. 왜 이렇게 꼼수로 하냐면... 귀찮기 때문이긴 하지만 그렇게 말하면 없어보이니까 게임의 긴장감을 위해서라고 해두도록 하자(찡긋)
게임에 맞게 조정
지금의 진자운동만으로도 진자 시뮬레이션 자체는 그럴싸하게 완성됐다. 애초에 진자운동은 진폭과 진자 길이와 중력 가속도만 고려하면 되는거니까. 하지만 이대로 게임에 사용하면 캐릭터는 계속해서 아래로 내려가기만 할 뿐 절대로 위로 올라갈 수가 없다. 진자의 최고점보다 높이 올라갈 수가 없기 때문이다.
그러면 게임이 너무 루즈해지는 단점이 있는데다가 쫄깃한 손맛 없이 왠지 답답한 조작감에 짜증이 나게 마련이다. 어차피 우리가 만드는게 무슨 과학교재도 아니니까 게임의 재미를 위해 조금 조정을 가해보자.
먼저 줄을 걸었을 때 확 잡아채는 맛이 생기도록
setPivot메소드에서 줄을 거는 순간의 초기 가속도 구하는 데다가 MSG를 좀 치자. 원래 -1 을 곱했지만, 좀 더 초기 속도가 빨라지도록 -1.3 정도를 곱하는 걸로 바꿔주자.
this.accel = (-1.3 * (this.force.x+this.force.y)/this.pLen) * Math.sin(this.angle);
그리고 진자를 놓고 점프하는 순간에도 약간 탄력받는 느낌을 살리도록 force에 양념을 좀 치자.
this.force.x *= 1.2;
this.force.y -= 1.5;
일단 앞뒤로 움직이는 힘을 1.2배로 곱해줬다. (그러면 앞으로 빨리 가고 있었을 수록 더 많이 탄력받아서 쓩~ 날아갈 수 있게 되겠지?)
그리고 y 축 힘에 -1.5를 더해줬다. y 축 힘은 음수인 경우 위로 올라가는 힘이되니까 약간 점프력을 보태준다고 생각하면 된다.
적절한 수치는 각자 알아서 찾아보도록 하자. 이리저리 해본 결과 이정도가 너무 쉽지 않으면서도 열심히 하면 위로 올라갈 수는 있는 좋은 한계치인 것 같다.
캐릭터 애니메이션
여지껏 빨간 동그라미만 움직여왔는데, 초반에 열심히 만든 스프라이트니 애니메이션이니 이딴걸 대체 언제 써먹는건지 의문이었다면 드디어 써먹어볼 때가 왔다.
우선 아래 이미지를 가지고 캐릭터의 애니메이션을 만들어보자. 아래 이미지에는 이후로도 사용될 대부분의 스프라이트들이 포함되어 있다.. 그리고 저작권은 아마도 네오플에 있을거다. (사실 잘 모르지만 아마 그럴거임.. 근로계약서 꺼내보기 귀찮다. 네오플에 없어도 어쨌든 나한테는 있으니 상업적 이용은 하지 말 것...어따 쓰겠냐마는.)
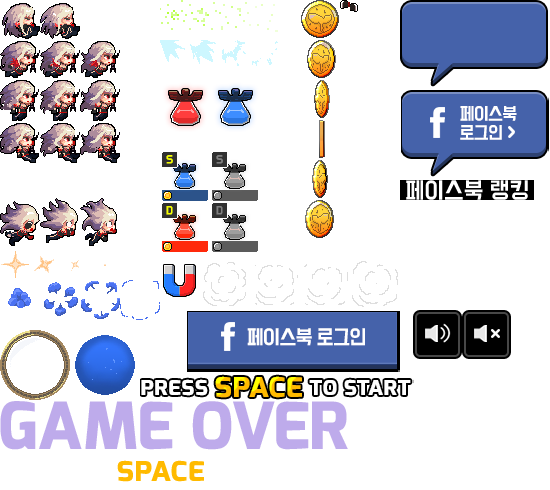
1편에서 우리가 만든 스프라이트 구조와 애니메이션 구조들은 기억할테니 거기에 맞게 스프라이트들을 정의해보자. 스크립트 맨 위쪽에 아래와 같이 스프라이트 정의와 애니메이션 정의를 추가한다.
const SpriteDefs = {
"character":[
{x:0,y:0,w:40,h:40,origin:{x:20,y:20}},
{x:40,y:0,w:40,h:40,origin:{x:20,y:20}},
{x:0,y:40,w:40,h:39,origin:{x:30,y:20}},
{x:40,y:40,w:40,h:39,origin:{x:30,y:20}},
{x:80,y:40,w:40,h:39,origin:{x:30,y:20}},
{x:0,y:80,w:40,h:41,origin:{x:30,y:20}},
{x:40,y:80,w:40,h:41,origin:{x:30,y:20}},
{x:80,y:80,w:40,h:41,origin:{x:30,y:20}},
{x:0,y:122,w:40,h:41,origin:{x:30,y:20}},
{x:40,y:122,w:40,h:40,origin:{x:30,y:20}},
{x:80,y:122,w:40,h:40,origin:{x:30,y:20}},
{x:0, y:186,w:40,h:59,origin:{x:20,y:39}},
{x:40, y:186,w:40,h:59,origin:{x:20,y:39}},
{x:80, y:186,w:40,h:59,origin:{x:20,y:39}},
{x:340, y:0, w:18,h:12,origin:{x:9,y:6}},
{x:200,y:260,w:50,h:50,origin:{x:25,y:25}},
{x:250,y:260,w:50,h:50,origin:{x:25,y:25}},
{x:300,y:260,w:50,h:50,origin:{x:25,y:25}},
{x:350,y:260,w:50,h:50,origin:{x:25,y:25}}
]
};
const AnimationDefs = {
"character":{
"spin":[{frame:0,duration:0.05}, {frame:1,duration:0.05}],
"forward":[{frame:2,duration:0.08}, {frame:3,duration:0.08},{frame:4,duration:0.08},{frame:3,duration:0.08}],
"nutral":[{frame:5,duration:0.05},{frame:6,duration:0.05},{frame:7,duration:0.05},{frame:6,duration:0.05}],
"backward":[{frame:8,duration:0.05},{frame:9,duration:0.05},{frame:10,duration:0.05},{frame:9,duration:0.05}],
"fall":[{frame:11,duration:0.05},{frame:12,duration:0.05},{frame:13,duration:0.05},{frame:12,duration:0.05}],
"sword":[{frame:14,duration:1}],
"magnet_field":[{frame:15,duration:0.05},{frame:16,duration:0.05},{frame:17,duration:0.05},{frame:18,duration:0.05}]
}
};
스프라이트 정의를 보면 알겠지만 각 스프라이트들은 이미지에서의 위치/크기/중심점 좌표 정보를 가지고 있고, 각 애니메이션들은 각 프레임의 스프라이트 번호와 지속시간을 가지고 있다.
그럼 이 정보들을 바탕으로 스프라이트와 애니메이션을 생성해보자.
Character.constructor를 아래처럼 수정한다.
constructor(){
this.img = new Image();
this.img.src = "images/sprites.png"; //각자 자신의 이미지 주소를 넣자
this.spriteSheet = new SpriteSheet(this.img, SpriteDefs.character); //캐릭트 스프라이트 시트
this.animations = {}; //애니메이션들을 모아둘 컨테이너
//애니메이션 정의에 맞춰서 컨테이너에 애니메이션을 생성해서 넣는다.
for(let i in AnimationDefs.character){
if( !AnimationDefs.character.hasOwnProperty(i)) continue;
this.animations[i] = new Animation(this.spriteSheet, AnimationDefs.character[i]);
}
}
그리고 현재 어떤 애니메이션이 필요한지를 나타내는 변수를
init 에 추가하자.
this.currentAnimation = "forward";
그 후엔 상태에 따라 애니메이션을 변경하는 코드를
update에 넣어보자.
일단 공중에 있는(줄이 걸려있지 않은) 상태일 때는 'spin' 애니메이션이 나타나고, 줄에 매달려서 앞으로 갈 때는 forward, 뒤로 갈 때는 backward, 가운데쯤에서는 nutral 이 나오게 해보자. 이 부분은 force 의 x 값에 따라 판별하면 되겠지?
update를 아래처럼 수정한다.
update(timeDelta){
// 캐릭터의 각종 상태를 변경하는 부분.
if(this.pivot === null){
// 줄이 걸려있지 않을때
this.currentAnimation = "spin"; //현재 애니메이션은 spin 으로
this.force.y += this.gravity * timeDelta;
this.x += this.force.x;
this.y += this.force.y;
}else{
// 줄이 걸려있을 때
// 중력은 작용하고 있지만 각가속도 계산에 들어가므로 force.y 에 별도로 더해줄 필요가 없다.
let ang = this.angle;
let ang_vel = (-1*this.gravity/this.pLen) * Math.sin(ang); //각가속도
// 현재 각가속도에 경과시간을 곱해서 전체 각가속도에 합산
this.accel += ang_vel * timeDelta;
// 계속 같은 높이로 흔들릴 수는 없으니 시간이 흐를수록 가속도를 줄여준다.
// 현실로 치자면 줄의 마찰력이나 공기저항에 대한 시뮬레이션이라고 볼 수 있겟지?
this.accel *= 0.999;
// 그럼 이제 다음번 각속도 계산을 위해 현재 각도를 바꿔주고
ang += this.accel;
if( Math.abs(Math.rad2deg(ang)) >= 90 ){
this.setPivot(null);
}else{
this.angle = ang;
// 각 성분으로 분해해서 force에 할당하자
this.force.x = this.pLen * this.accel * Math.cos(ang);
this.force.y = -this.pLen * this.accel * Math.sin(ang);
this.position.x += this.force.x;
this.position.y += this.force.y;
this.x = this.position.x + this.pivot.x;
this.y = this.position.y + this.pivot.y;
}
if(this.force.x < -3){ this.currentAnimation = "backward"; }else if(this.force.x > 3){
this.currentAnimation = "forward";
}else{
this.currentAnimation = "nutral";
}
}
this.animations[this.currentAnimation].update(timeDelta);
}
그럼 이제
render에서 현재 애니메이션을 그려주면 되겠지?
render(ctx){
// 여기서 그려주면 된다.
// 일단은 현재 위치에 반지름 20픽셀 짜리 빨간 원을 그리는 코드를 넣어보자.
ctx.save();
if( this.pivot !== null ){
ctx.strokeStyle = "blue";
ctx.beginPath();
ctx.moveTo(this.pivot.x, this.pivot.y);
ctx.lineTo(this.pivot.x+this.position.x, this.pivot.y+this.position.y);
ctx.stroke();
}
ctx.translate(this.x, this.y);
ctx.fillStyle = "red";
ctx.beginPath();
ctx.arc(0, 0, 20, 0, 2*Math.PI); // 각도는 늘 라디안이라는 점을 잊지 말자!
ctx.fill();
ctx.fillStyle = "black";
ctx.fillRect(0, 0, 2, this.force.y*20);
ctx.fillRect(0, 0, this.force.x*20, 2);
ctx.restore();
this.animations[this.currentAnimation].draw(ctx, this.x, this.y, {});
}
여기까지 진행했으면 아래처럼 캐릭터가 살아 숨쉬게 된다! 우왕!굳!
또 글이 너무 길어지니까 다음 편에서 만나도록 하자능! 헤헿